




Since the E-CRISPR system involves the reaction of the nucleic acid chain on the interface between the solution and the screen-printed electrode plate, and the electrical signal conversion process generated by the reaction, it is very different from the state (appearance and characteristics) of the electrode plate itself. There are huge difficulties in theoretical modeling, so this part focuses on simple data processing.
Figure 1: Though modification of the G nucleic acid chain with methylene blue fluorescent group on the screen-printed electrode, and then using the electrochemical workstation to measure the volt-ampere signal change on the electrode plate after 8hr, 10hr, 24hr, and 36hr, it can be seen that there is no obvious peak in the current signal in 8 hours after 10 hours, indicating that the chain modification has not been fully completed at this time and the interface is still unstable. From 24 hours to 36 hours, the peak height increased significantly, indicating that the G chain is indeed constantly modifying onto the surface of the electrode plate, and the longer the time, the more and more stable the modified chain are on the electrode plate.

Cutting the G chain with the inactivated Cas9 nuclease at the HNH site will produce changes in the current signal. A batch of plates that have been modified for 24 hours was tested for voltammetric signals (Figure 2). It was found that although the electrical signals generated on different plates were different in size, the amplitude and trend of the signal change are the same. Besides, a continuous test of the voltammetric signal on the same electrode plate which has undergone a 36-hour modification of the G chain (Figure 3) found that the peak position was stable, the peak height was continuously reduced, and the signal was continuously attenuated, that is, the speed of the enzyme digestion reaction was continuously reduced.


G chain modification occurs on the surface of the electrode, and a chemical reaction occurs between the nucleic acid chain and the electrode plate, and electrons are transferred to generate electrical signals. The more chains are combined on the plate, the stronger the current signal can be seen. There are two types of plates used in the experiment, and the difference lies in the size of the electrode. Set two gradients of the duration of binding nucleic acid strands on the two plates, as shown in Figure 4. It can be seen that as the seed strand time increases, the current signal has an upward trend, which confirms that the number of strands does increase with the passage of time.

If the G chain modification is a stable accumulation process on the surface of the electrode plate, the elution in the chain modification stage will show a substantially linear elution curve with increasing time. Use buffer for the electrode plate after the chain modification lasts for 8 hours. When the elution time continues to increase, the voltammetric signal is tested (Figure 5), and the data is fitted to obtain the logistic equation instead of simple linearity. It may be that chain modification is not a simple amount accumulation, and the G chain may not all be inserted straight on the plate. Some chains may lie on the plate or entangle each other, which is difficult to elute, thus affecting the current signal.


Combining the C chain complementary to G to the G chain that has been planted on the plate, adding Cas9 nuclease, etc., a cleavage chemical reaction can occur, and the peak signal is significantly attenuated. After testing 7 sample plates, it is found that the attenuation ratio of current signal is concentrated in 30%~60%. We believe that the attenuation in the range of 30%~50% is reliable. (Figure 6)


Reaction Kinetic Model
1.Foundation of model building

2.Principles of stepwise chemical reactions


Figure 1: After the magnetic beads are assembled, a L-O-ABC composite structure is formed. The three ABC chains form a stable sandwich structure. Under the microscopic view, the B chain will have a very small amount of dissociation equilibrium, but it cannot be measured by PAGE gel electrophoresis.


Figure 2: After adding the T and W chains to the system, T fixes the W-α port on the L chain, the W-β end and C undergo a Toehold1-mediated chain displacement reaction, and the W-β end replaces the B chain. The balance moves to the right.
Since the binding domains of W-β and B are both 19bp in length, ΔH=0, and the binding of W-β to the AC structure belongs to intramolecular binding, the released B chain is freed, and the number of molecules increases from 1 to 2. Increase, ΔS>0, that is, ΔG=ΔH-TΔS<0, it is a spontaneous reaction. It can be seen that the structural stability is LTW-O-ACW>L-O-ABC.
Since the binding domains of W-β and B are both 19bp in length, ΔH=0, and the binding of W-β to the AC structure belongs to intramolecular binding, the released B chain is freed, and the number of molecules increases from 1 to 2. Increase, ΔS>0, that is, ΔG=ΔH-TΔS<0, it is a spontaneous reaction. It can be seen that the structural stability is LTW-O-ACW>L-O-ABC.
Figure 3: Without the fixation of T, the W chain cannot be connected to the L, and the intramolecular base complementary pairing of W itself forms a hairpin secondary structure, that is, the LTW composite structure cannot be formed, and the W and the magnetic bead complex no longer form a single-molecule-like whole structure. In other words, replacing B with W does not increase the number of molecules, nor does it increase the length of the binding region, so there is no competitive advantage, ΔH=0, ΔS=0, the reaction cannot proceed spontaneously, and the structural stability L-O-ACW≤L-O-ABC.



Figure 4: Adding the F chain to the system, F will affect the ACW composite structure, replace C from A and W to form a CF composite chain, release the W-β end, perform the next replacement, and the reaction balance will shift to the right.
Since the AC binding domain is 16bp in length, CW binding domain is 19bp in length, CF binding domain is 29bp in length, ΔH<0; the number of molecules does not increase or decrease, ΔS=0, that is, ΔG=ΔH-TΔS<0, structural stability CF>LTW-O -ACW.
3.The total chemical reaction equation
Throughout the process, F quantitatively competes with C from the composite structure. W is first consumed by the reaction and then formed, acting as a catalyst. T plays a role of fixing W, but does not actually participate in the reaction. The general equation is

According to 1.1 analysis, the structural stability is summarized as

However, the structural stability is relative to a specific reaction, and the reaction direction and rate cannot be directly estimated. For example, the C chain can quickly replace the W-β end in the ACW composite structure, and it directly replaces the C chain in the ABC composite structure. The rate is slower than the rate at which W-β replaces the B chain.
4.Kinetic equation construction
In order to meet the need of simplification, the total chemical reaction equation is approximated as a second-order confrontation reaction, namely

if F is not excessive, set the initial concentration of L-O-ABC and F at time 0 to a and b, respectively, the concentration of CF at time 0 is 0, and the concentration of CF at time t is x, that is, for the reaction, the consumption rate of F is

Set a=b, then when balanced

integral

Points get

5.Experimental design based on reaction order


During the reaction, the B chain will fall off spontaneously and form a dissociation equilibrium, but this equilibrium is very weak and almost covered by the main reaction. Because F will be added in excess in the main reaction, it is difficult to directly measure the consumption rate of F and it is difficult to accurately quantify it, so the generation rate of CF complex can be used instead. For example, when a fluorescent group is mounted on the 3'end of the C chain, when C is stably bound to A, the fluorescent group is affected by the magnetic field of the magnetic beads and the fluorescence is quenched. Once F replaces C into the solution and moves away from the magnetic beads, it is quenched The function is invalid, the fluorescent signal is visible, and real-time monitoring is performed, which saves time and effort. (Figure 5)

Figure 6: The ABC composite structure and the LTW composite structure are modified on avidin. There is a quantitative relationship between the binding of the two complexes on avidin. The same avidin molecule can modify 0~4 ABC complexes. Structure or LTW composite structure. For the sake of calculation simplicity, it is now assumed that the biotin-nucleic acid composite structure joined on the same avidin molecule is the same structure, that is, the situation in the upper right corner of figure 6.

Figure 7: A very large number of avidin molecules can be loaded on the same magnetic bead, and they are evenly distributed on the spherical surface. Several nearest avidin molecules are combined on the spherical surface to form a spherical micro-unit. The spatial extension of avidin and biotin is much smaller than the length of the nucleic acid chain, which can be approximated as a point attached to the spherical surface with no actual height. The four chains on the sphere approximately form a quadrangular pyramid. This quadrangular pyramid can rotate around the avidin molecule and the normal direction of the sphere to produce a cone-shaped envelope surface, which is essentially the coincident surface of the respective envelope surfaces of the four chains. The interface of the micro-unit is very small, approximately flat. The length of the generatrix of the cone envelope surface is fixed, but the cone apex angle is variable, and the circle cluster composed of the edge line envelopes into an approximate hemisphere. In a micro unit, if the spheres do not intersect, the two complexes will not compete for displacement; after the tangent to the intersection, the β end of the W chain can enter the motion space of the A-B-C complex, and strand displacement will occur.
Figure 8: Since W can react with multiple ABC complexes, the number of W chains should be as small as possible in the same reaction zone to ensure that the amount of L chains is as small as possible when the content of T chains is unknown. According to the envelope surface model, W-β can replace C-toehold1 of multiple ABC complexes in the same area, such as 3 or 4. The purple spherical surface represents the W-β end envelope surface, and the blue spherical surface represents the C-Toehold2 end envelope surface.


If the equilateral triangle distribution scheme is adopted, it means that one W sphere area can be chain-replaced with the surrounding 3 ABC complex sphere areas, and one ABC area can be chain-replaced with the surrounding 6 W areas. Since each sphere includes four chains, the number of ABC compound chains that each W may be allocated is calculated as

The number of W chains that each ABC complex may be exposed to is calculated as

In the same way, the square distribution scheme is adopted, which means that one W spherical area can be chain-replaced with the surrounding 4 ABC complex spherical areas, and one ABC area can be chain-replaced with the surrounding 4 W areas. Since each sphere includes four chains, the number of ABC compound chains that each W may be allocated is calculated as
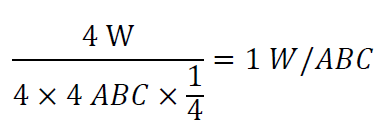
Other types of distribution can be analogized. It can be seen that the more ABC areas that a group of W areas can touch, the more ABC that can be replaced by each W, and the lower limit of distribution replacement should be 0.5 ABC/W, because the contact area is less than 3 meaningless. That is, the lower limit of the ratio of the ABC mounting capacity to the W mounting capacity should be 1:2.

Figure 9: Calculate the amount of A and L chains required for magnetic bead assembly from the theoretical geometric model. It is known that the space extension length of 10 bp base pair is 3.38 nm, and the diameter of the magnetic beads is 100 nm (the space length of avidin and biotin has been ignored). Since W and C want to pair, at least a 19bp length matching area is required. Therefore, the radius of the outer envelope of the complex ABC is at most 31 bp (10.48 nm), and the radius of the outer envelope of the LTW complex is at most 85 bp (28.73 nm). ), the maximum distance between two avidins is 39.21nm.

Figure 10: The maximum distance between two avides is 2/3 of the height of the equilateral triangle, from which the area of the triangular micro-unit can be calculated as
The magnetic bead particles are spheres, according to the sphere surface area formula

That is, the minimum number of avidins of LTW composite structure that can be bound on a single magnetic bead is

Figure 11: The calculation result of the model approximately conforms to the structure of a regular icosahedron, but each vertex of the regular icosahedron is the intersection of 5 regular triangles. The original model draws a spherical regular triangle into a plane triangle to simplify the calculation, which is different from the actual result. Therefore, the model needs to be revised.

One W sphere area can be chain-replaced with the surrounding 3 ABC complex sphere areas, and one ABC area can be chain-replaced with the surrounding 5 W areas. Since each sphere includes four chains, the number of ABC compound chains that each W may be allocated is calculated as

The number of W chains that each ABC complex may be exposed to is calculated as

The binding quantity of avidin of LTW complex is 20 per magnetic bead, and the binding quantity of avidin of ABC complex is 12 per magnetic bead, for a total of 32 avidins per magnetic bead. That is, the total molecular weight of avidin on a single magnetic bead is

With reference to the magnetic bead density of 2.3 g/cm3 in the relevant information, the total amount of magnetic beads per milliliter of magnetic bead suspension is

Then the amount of avidin material required per milliliter of magnetic bead suspension is at least

That is, the minimum avidin load required per milliliter of magnetic bead suspension is


The calculation of the upper limit of assembly is based on the condition that the magnetic beads are fully saturated and the same avidin molecule can only modify the same kind of complex chain. Different from the lower limit calculation, the upper limit calculation uses the inverse method.
The saturated avidin loading capacity per milliliter of magnetic beads is

The amount of saturated avidin per milliliter of magnetic beads is

The number of avidin assembled on each magnetic bead is

Divide the sphere into 3526 approximate plane geometric triangles, each with an area of

It is necessary to determine the base and height of the triangle. For the convenience of calculation, the plane triangle is still approximated as an equilateral triangle, and the side length of the equilateral triangle is

The model is calculated on the condition of a standard plane equilateral triangle. The actual divided triangular micro-units may not meet the assumptions of equilateral triangles, so the error needs to be calculated. If the error is small, the above model can be used. The method of model checking and correction is linear programming.
Figure 12: Imagine the magnetic bead as a perfect sphere of the earth. The sphere is divided into 3526 equilateral triangles. The y_0 latitude line (equator) is approximately a positive X side, and the x_0 longitude line (a circle formed by the prime meridian and 180° longitude) Approximately a regular 2Y side type, the height of the triangle is H, and the side length is A, then the equilateral triangles divided into a spherical surface need to satisfy the following relationship

If X and Y are not treated as positive natural numbers temporarily, X=69.25 and Y=39.98 calculated by A, then X and Y can be rounded up and down. The calculation results are listed as follows

It can be seen that when X=69 and Y=40, the error between this division and the ideal equilateral triangle division is 0.4%, and the original hypothesis can almost be considered reasonable, that is, the equilateral triangle division can be considered reasonable, and it can indeed be used in the model calculation.

Figure 13: Now the center of each equilateral triangle is combined with an avidin molecule. The maximum radius of the circular surface obtained from section 2.3 is 39.21nm, and the number of equilateral triangle microcells that this circular surface can cover can be obtained. According to the plane drawing and geometric solution, the micro-elements that can be shielded by the circular surface are marked in the figure. The yellow triangle and the triangle on its right can be shielded by the circular surface, that is, 136.75 regular triangle micro-elements can be shielded in a quarter of a circular surface ( The boundary is calculated as 0.5, and the intersection is calculated as 0.25), then a complete circle can shield 547 micro-units, that is, if 1 avidin is combined with the LTW complex, it can affect the 546 avidin around it The bound ABC complex has the potential for strand displacement reactions.

In order to construct the model simply, it is approximated that the round surface on a magnetic ball sphere has

At least 6.5×4=26 LTW composite structures need to be hung on a magnetic bead, and at most 6.5×4×546=14196 LTW composite structures can be mounted on a magnetic bead. The data on the upper limit of the dosage in the reaction system is calculated as follows:

References:
[1] Li, L., Zhang, W., Tang, X., Li, Z., Wu, Y., & Xiao, X. (2020). Fine and bidirectional regulation of toehold-mediated DNA strand displacement by a wedge-like DNA tool. Chemical Communications. doi:10.1039/d0cc03722b [2] C.-P. Liang, P.-Q. Ma, H. Liu, X. Guo, B.-C. Yin, B.-C. Ye, Angew. Chem. Int. Ed. 2017, 56, 9077.